Linear Prediction Models
![]()
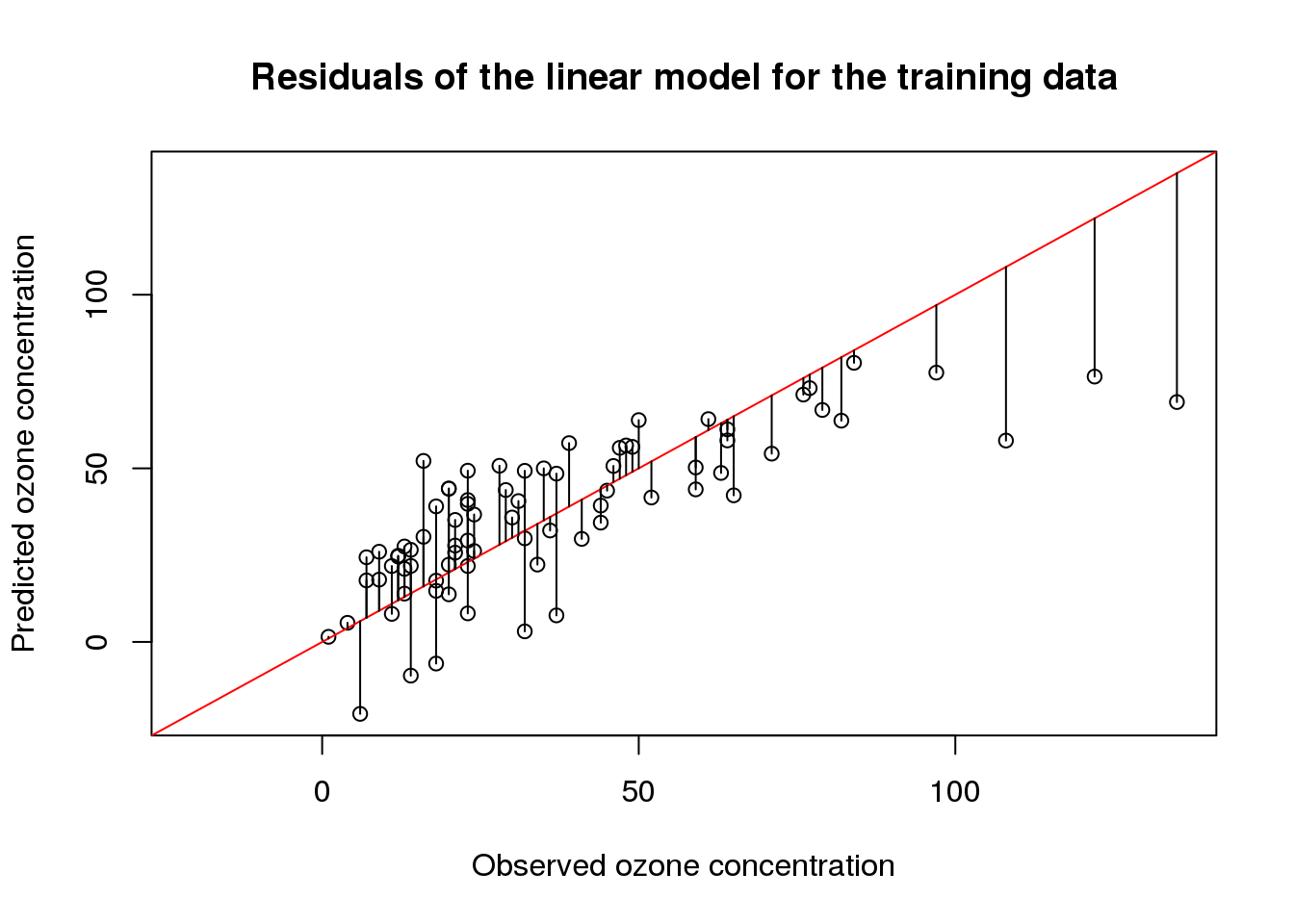
Linear prediction models assume that there is a linear relationship between the independent variables and the dependent variable. Therefore, these models exhibit high bias and low variance.
The high bias of these models is due to the assumption of nonlinearity. If this assumption does not sufficiently represent the data, then linear models will be inaccurate.
On the other hand, linear models also have a low variance. This means that if several linear models would be trained using different data, they would perform similarly on the same test data set. This is because linear models are inflexible because there are few parameters to be tuned.
Thus, linear models are interpretable and robust. However, if their assumptions are not met, they willl perform poorly.
When do use linear models?
Linear models excel under the following circumstances:
- There are few data available, which would lead to overfitting with more complex models.
- There are indications for a linear association between features and outcome.
- Interpretation rather than predictive performance alone is important.
Popular linear models
The following linear models are frequently used:
- Linear regression: the most basic linear model for regression.
- Logistic regression: a linear model that is suitable for classification.
- Generalized linear models: for specific applications other linear models such as Poisson regression may be appropriate.
- Ridge regression: a linear model for regression that is regularized using an \(L_2\) norm.
- Lasso regression: a linear model for regression that is regularized using an \(L_1\) norm.
- Support vector machines (SVMs): SVMs based on linear kernel functions correspond to linear, \(L_2\) regularized models relying on a hinge loss.
Posts about linear models
The following posts deal with linear models for prediction.

Interpreting Generalized Linear Models
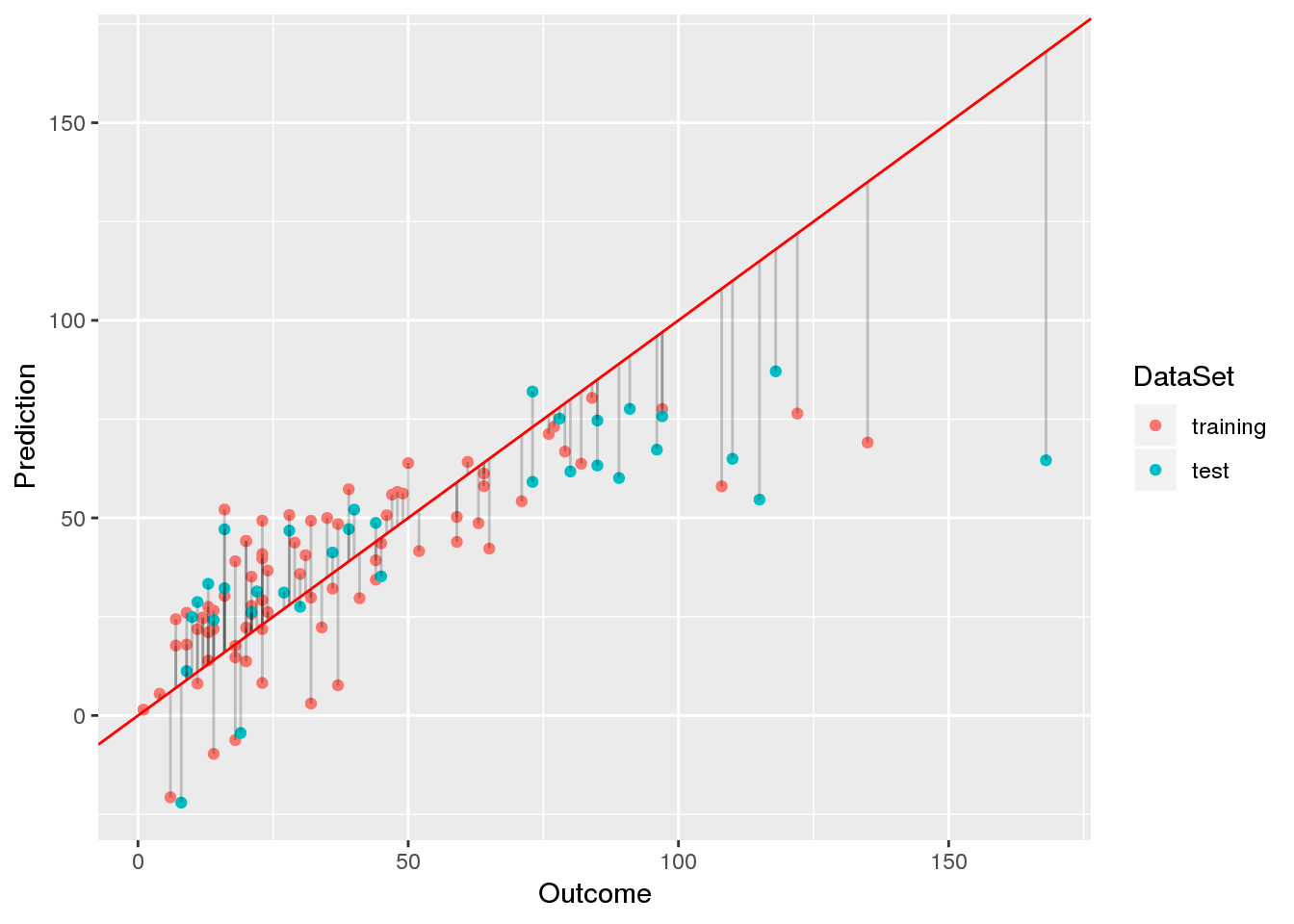
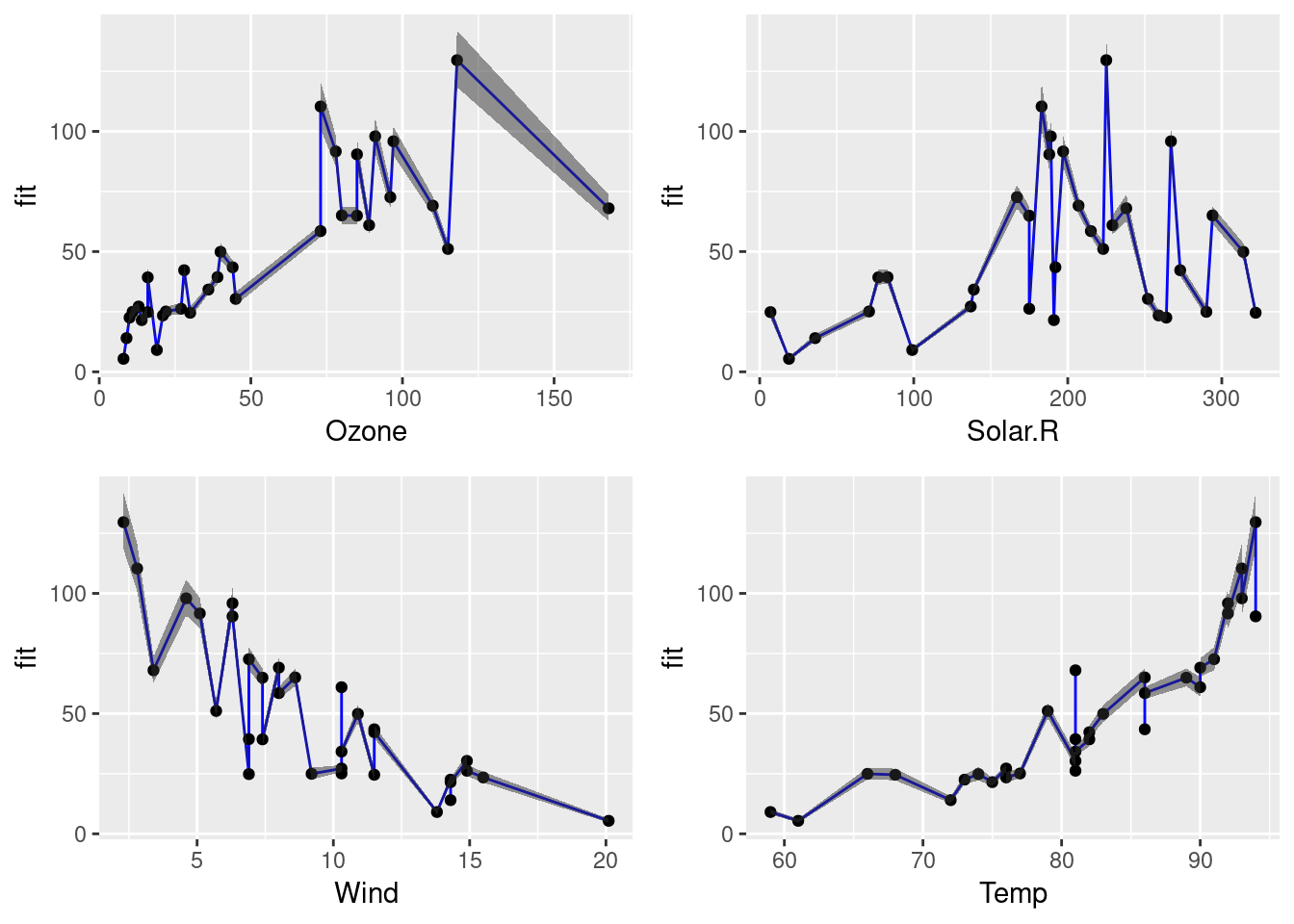
Finding a Suitable Linear Model for Ozone Prediction