R for applications in data science

All posts with the R tag deal with applications of the statistical programming language R in the data science setting.
Posts about R

Interpreting Generalized Linear Models
Finding a Suitable Linear Model for Ozone Prediction
Interpreting Linear Prediction Models
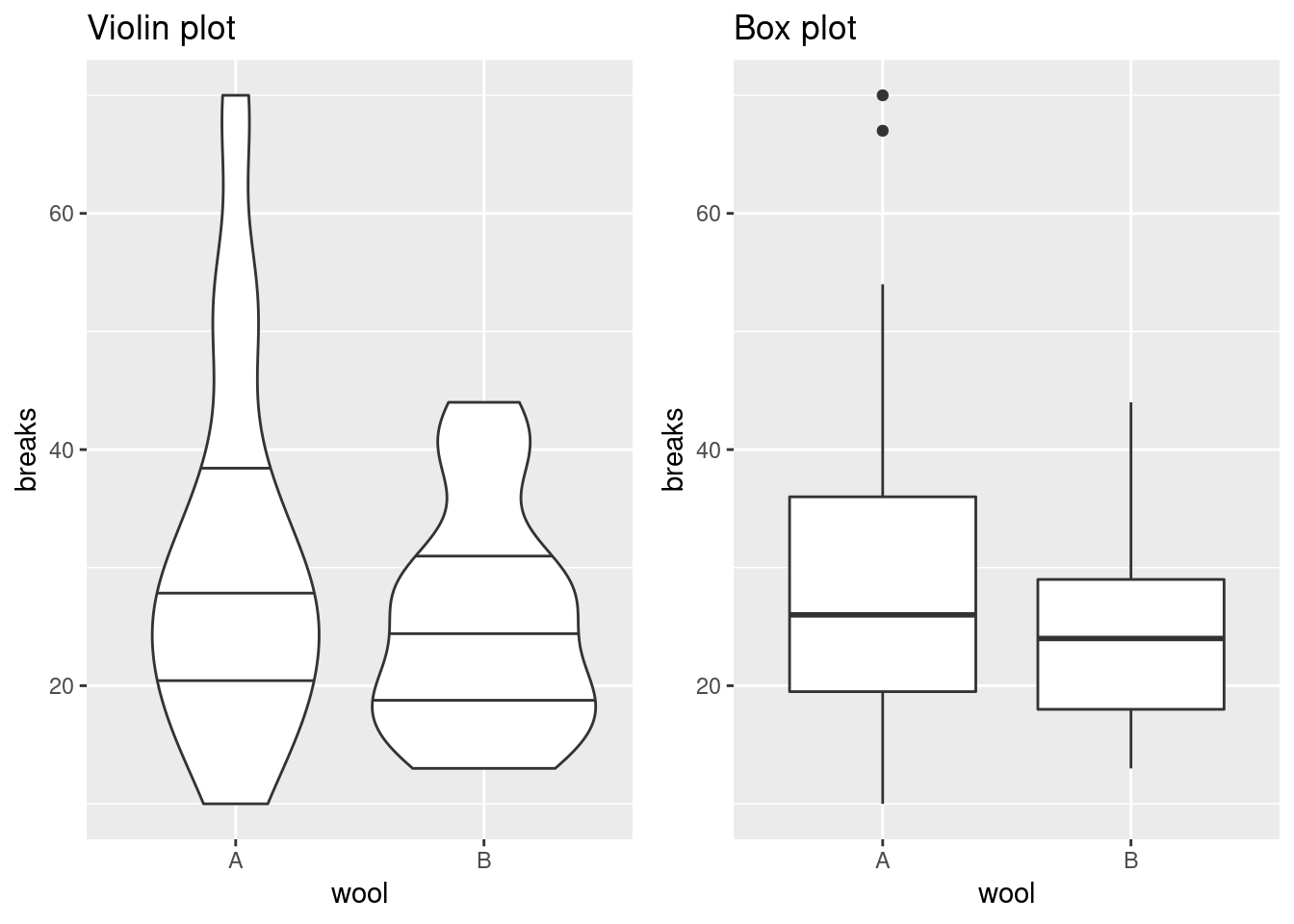
Box Plot Alternatives: Beeswarm and Violin Plots
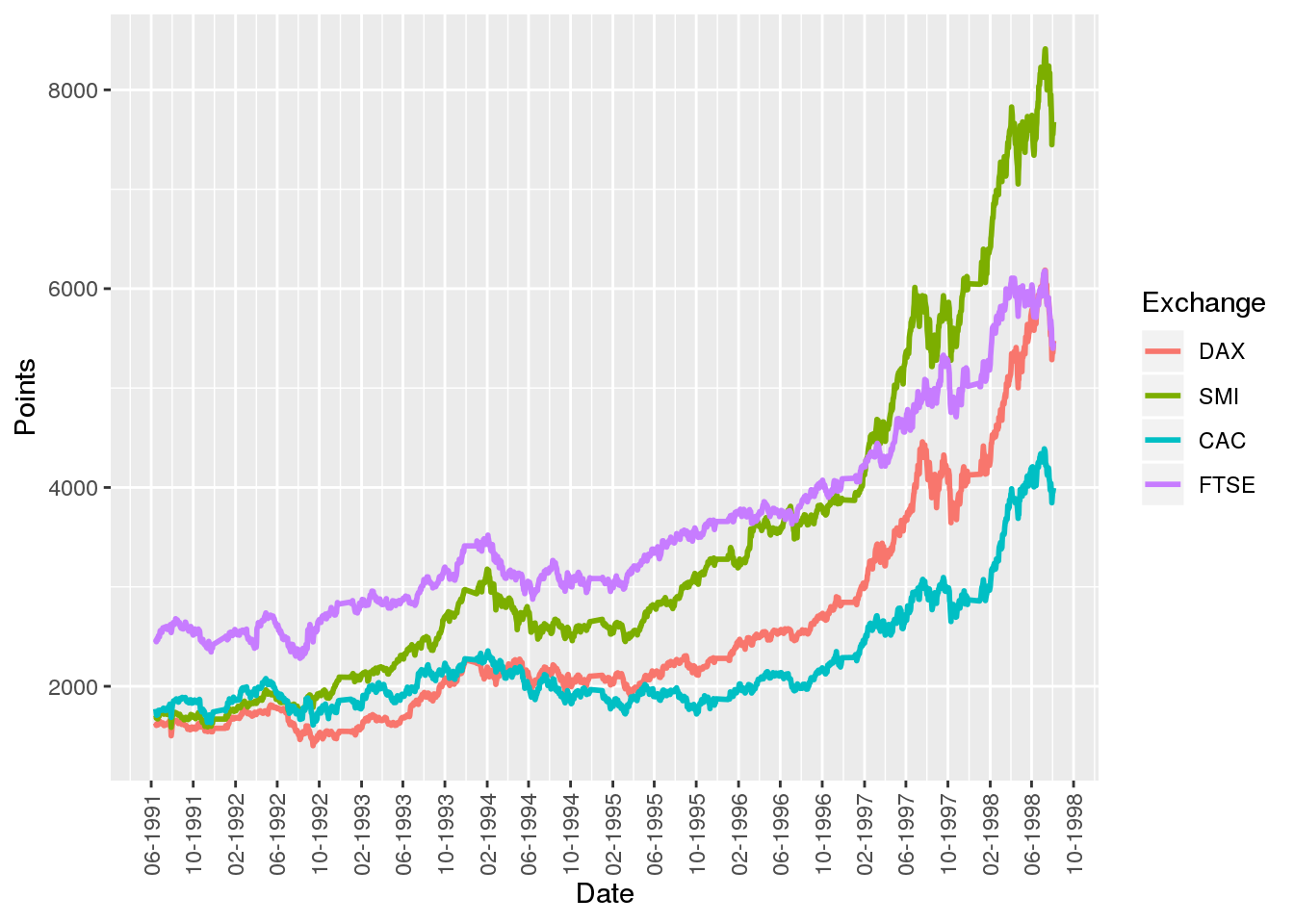
Visualizing Time-Series Data with Line Plots
The line plot is the go-to plot for visualizing time-series data (i.e. measurements for several points in time) as it allows for showing trends along time. Here, we’ll use stock market data to show how line plots can be created using native R, the MTS package, and ggplot.
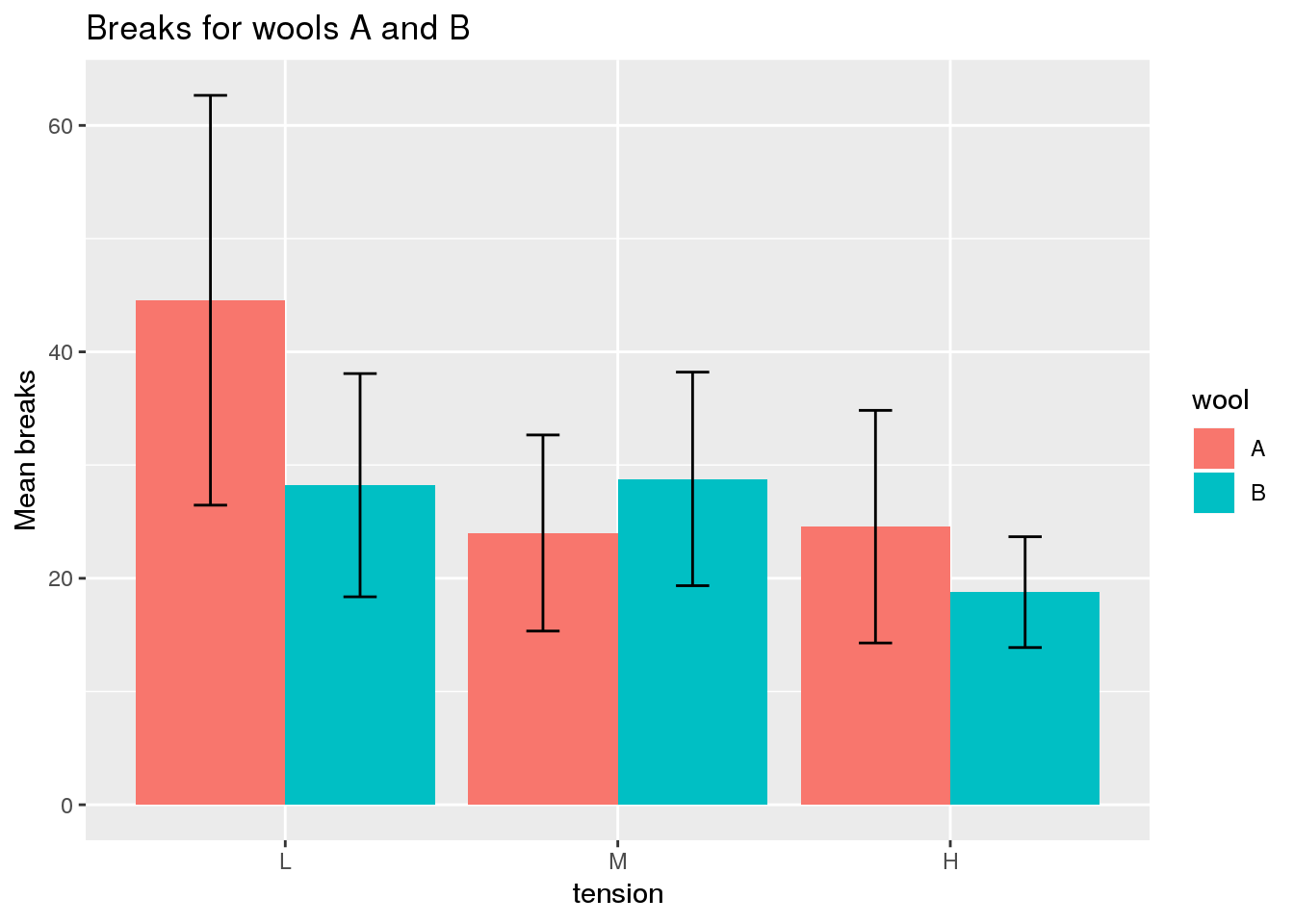
Bar Plots and Error Bars
Bar plots display quantities according to the height of bars. Since standard bar plots do not indicate the level of variation in the data, they are most appropriate for showing individual values (e.g. count data) rather than aggregates of several values (e.g. arithmetic means). Although variation can be shown through error bars, this is only appropriate if the data are normally distributed.
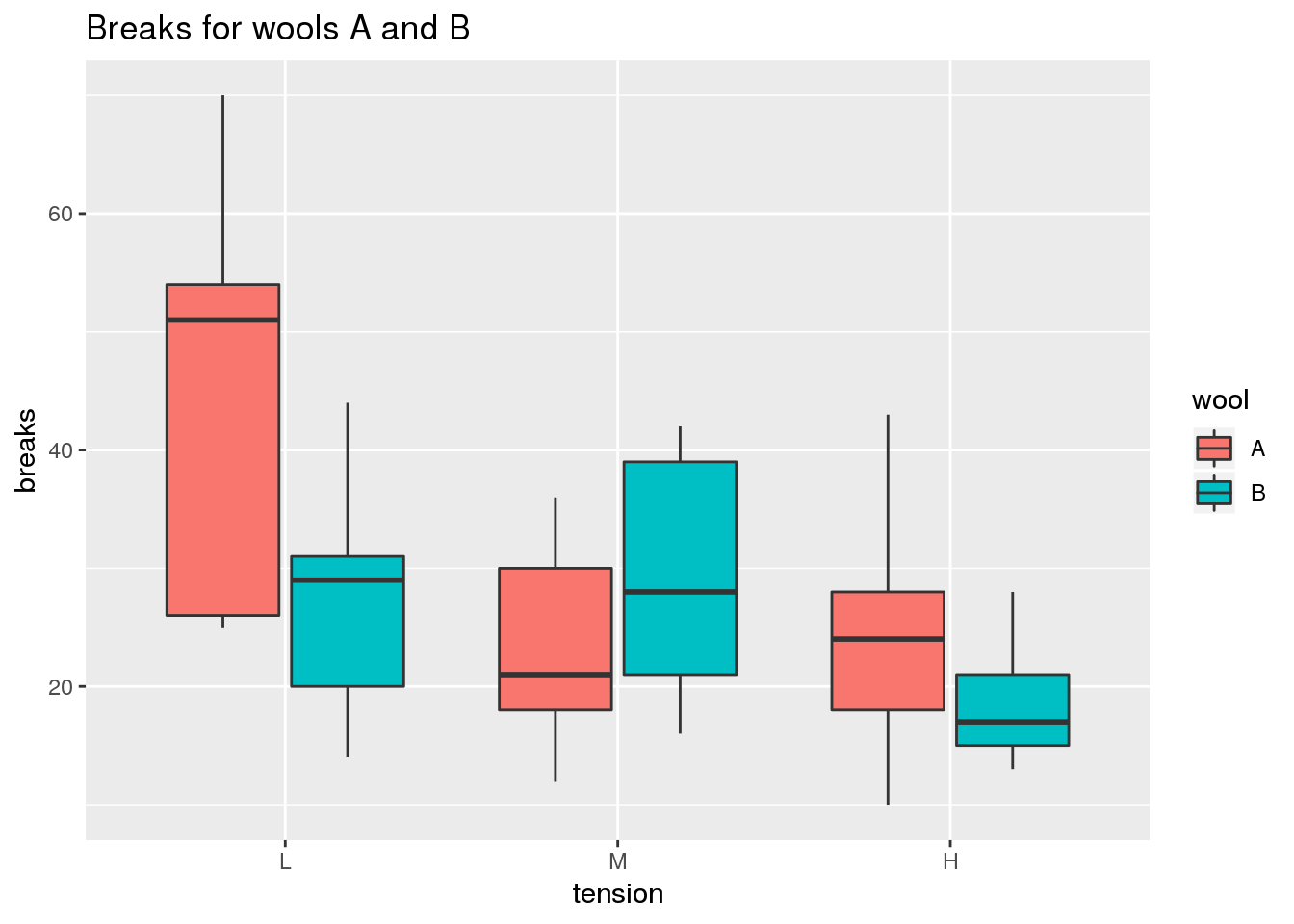
Comparing Medians and Inter-Quartile Ranges Using the Box Plot
The box plot is useful for comparing the quartiles of quantitative variables. More specifically, lower and upper ends of a box (the hinges) are defined by the first (Q1) and third quartile (Q3). The median (Q2) is shown as a horizontal line within the box. Additionally, outliers are indicated by the whiskers of the boxes whose definition is implementation-dependent. For example, in geom_boxplot of ggplot2, whiskers are defined by the inter-quartile range (IQR = Q3 - Q1), extending no further than 1.5 * IQR.
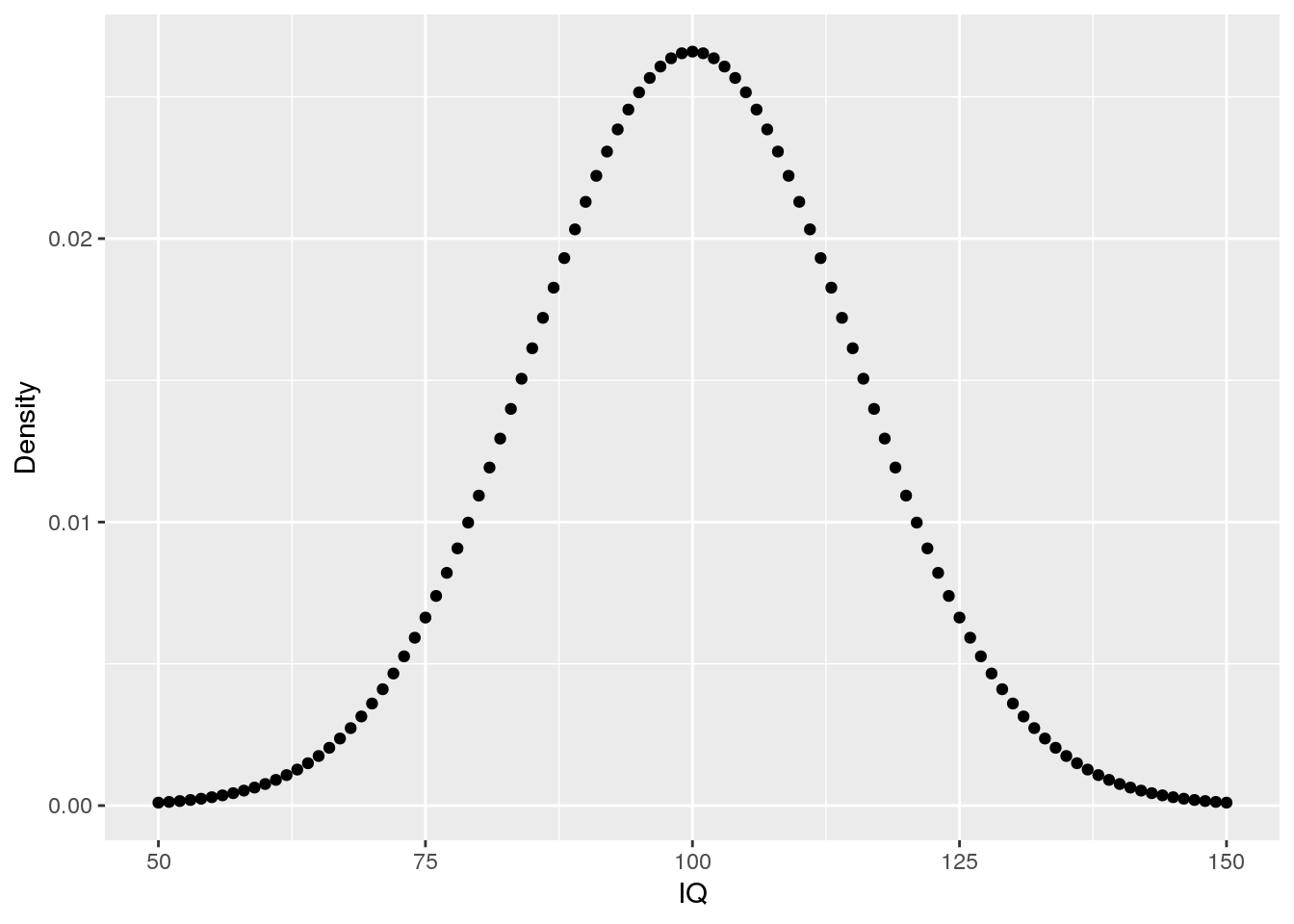
Using probability distributions in R: dnorm, pnorm, qnorm, and rnorm
R is a great tool for working with distributions. However, one has to know which specific function is the right wrong. Here, I’ll discuss which functions are available for dealing with the normal distribution: dnorm, pnorm, qnorm, and rnorm.
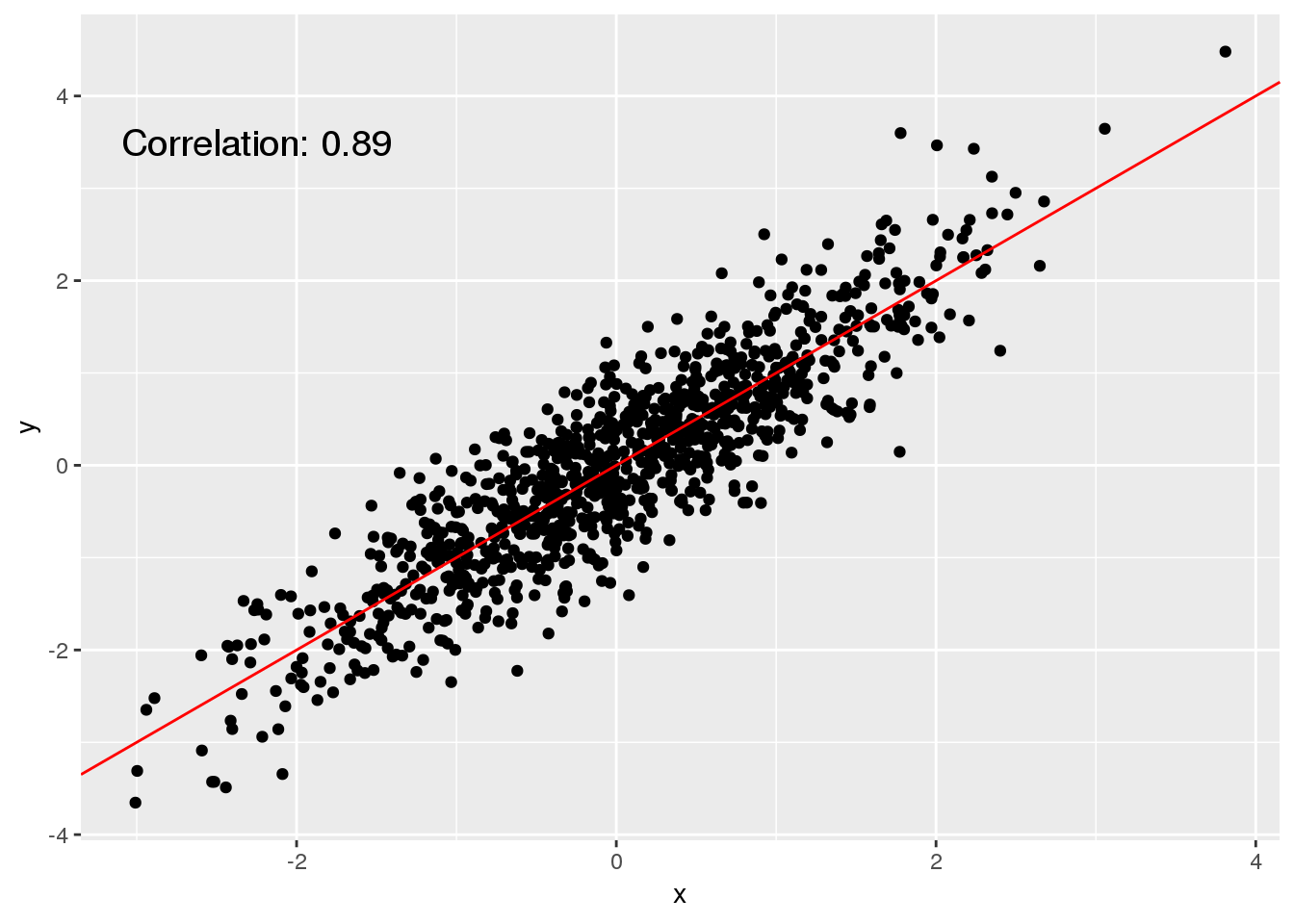
Visualizing Individual Data Points Using Scatter Plots
The scatter plot is probably the most simple type of plot that is available because it doesn’t do anything more than to show individual measurements as points in a plot. The scatter plot is particularly useful for investigating whether two variables are associated.


